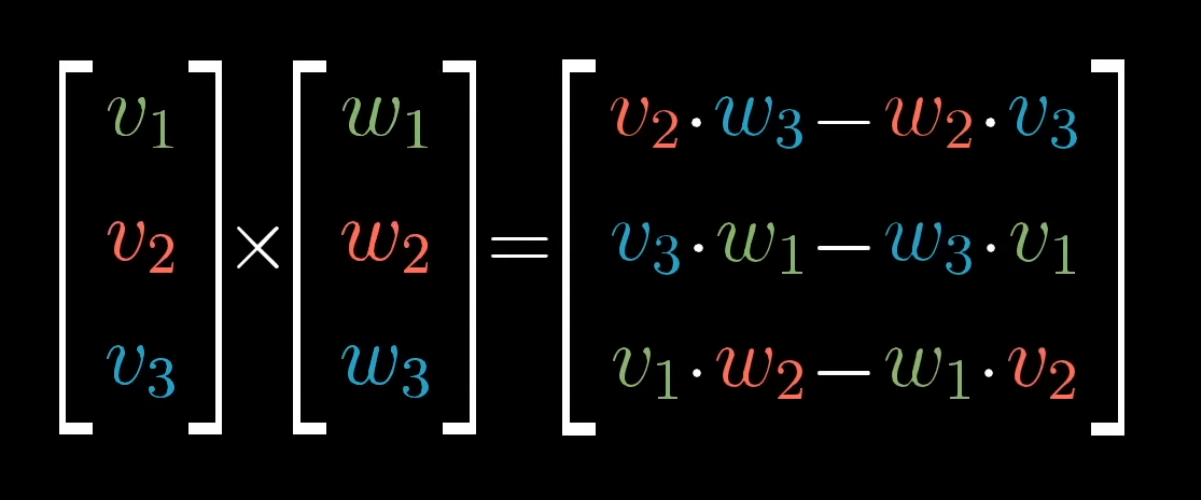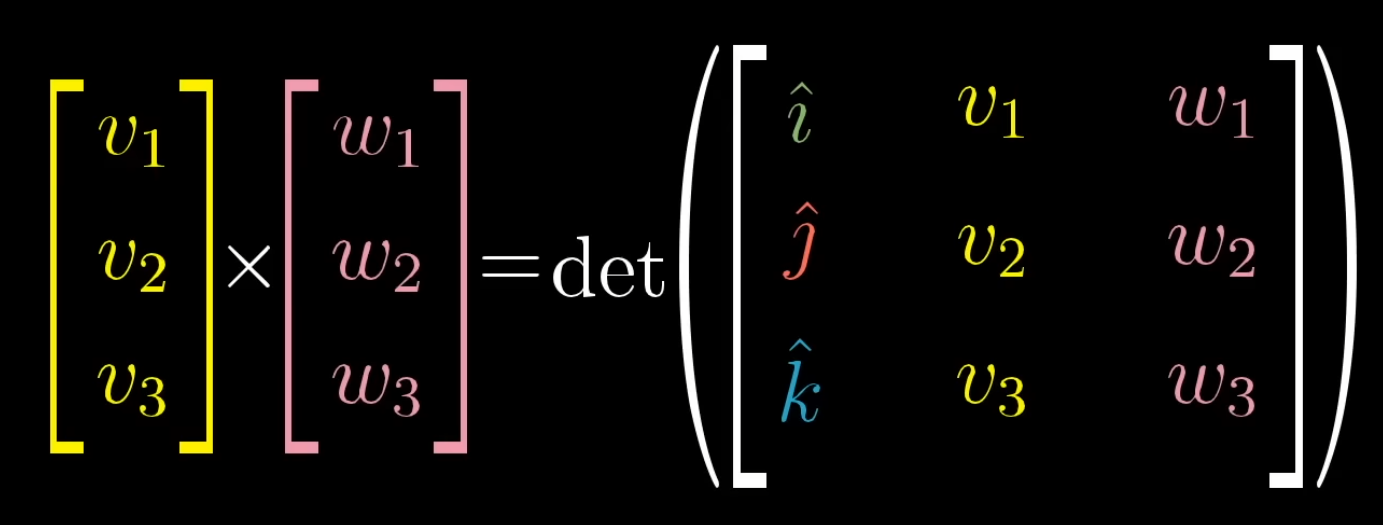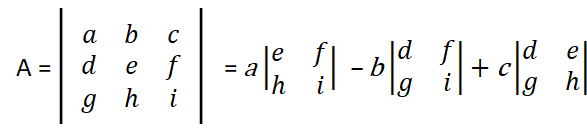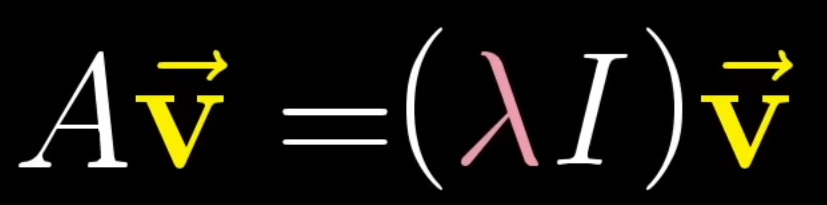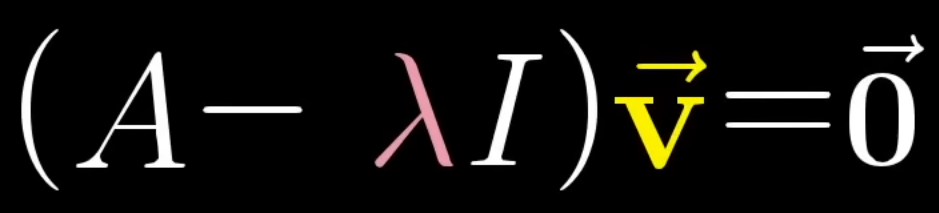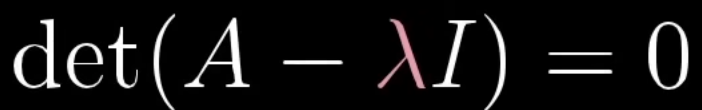Glossary
The following are terms to know in alphabetical order (not in an order that you should learn these concepts)
Basis Vectors
(Linearly Independent) Vectors that can be used to span the space of a coordinate system.
Example: The î vector in the X direction and the ĵ vector in the Y direction, are the basis vectors of of the XY coordinate system. You can specify coordinates in terms of the sum of 2 scalars each multiplying with a basis vector (Linear Combination). By having different Basis vectors, you can create alternate coordinate spaces
Change of Basis vectors / Transform in another basis
Take the alternate basis vectors v1 and v2 (and v3), and put them in a square matrix such that [v1, v2, (v3)], which we represent with A.
- To go from alternate space to standard space -> it is A * (input vector)
- To go from standard space to alternate space -> A-1 * (input vector)
Given transformation T in standard space, to find the effect of the same transformation matrix T on a vector of alternate space X in the alternate basis space A:
- A-1 * T * A * X
- in other words, transform their space vector to our space, apply our transformation, then transform back into the original space
- in this case, the outer A and A-1 matrices are known as the Empathy
Column Space
The set of all possible outputs of Av (transform A acting upon vector v) is known as the column space of A.
In other words, the span of the columns of A (treating each column of A as a basis vector)
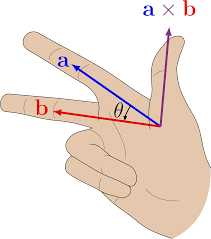
Cross Product
Given 2 vectors that define a plane, taking the cross product of those 2 vectors results in a new vector perpendicular from the plane established by the 2 input directors, with the length being determined by the area of the 2 input vectors (the determinate), and the direction being determined by the right hand rule.
(you can think of the i j k basis vectors as well).
Determinate
The scalar amount an area would expand by as a ratio after a linear transformation
- If a determinate is negative, it means the space flipped in on itself (in the case of 3D, the Left hand Rule flips to the Right hand rule, and vice versa)
- If a determinate is 0, then the transformation decreased the Span / dimensionality, because it squished space down such that the original area now becomes 0
- The determinate of the product of 2 matrices is equal to the product of the determinate of each those same matrices (independently)
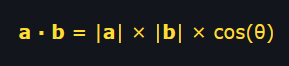
Dot Product
A way to "multiply" 2 vectors of equal length that outputs a scalar result that tells us about the angle between them.
- A positive result indicates they are pointing in the same direction
- A negative result indicates pointing in the opposite direction
- 0 means the vectors are perpendicular
Can be calculated in 2 ways:
- Multiplying each term (x with x, y with y, etc) of each vector together, than summing them up
- multiplying the length of each vector with the cosine angle between them
This implies that the angle between 2 vectors is the inverse cosine of the dot product of the 2 vectors all divided the by the product of the magnitudes of those vectors
(it also implies that if the product of the lengths equals the dot product, that the angle between them is 0)
Diagonal Matrix
Whenever a matrix is all 0's except down its diagonal
A transformation like this means that all the basis vectors (columns) are eigenvectors, and the numerical vector of each is their eigenvalue. These are also known as eigenbasis vectors
Diagonal matrices are easy computationally to work with. IE multiplying by a diagonal matrix on a vector is the same as multiplying the corresponding X or Y value with the respective eigenvalue to the power of the number of times multiplied
Eigenvectors / Eigenvalues
The Eigenvectors of a linear transformation are any vector that remains on their span during the linear transformation (IE they only are scaled, not change direction). The value of the eigenvector is the factor by which a vector on that span is scaled (also called eigenvalue)
Computation
General equation:
Where:
- A is the transform matrix
- v is an input output vector
- λ is the (scalar) eigenvalue
This equation states that applies transform A on v, is the same as scaling v by eigenvalue λ
this can also be written as
This means that some refactoring, we get this:
And as per the rules of determinate, any transform on a vector that results in 0, means that the determinate of that transform must be 0.
Trying to compute the determinate equal to 0, you end up with an equation (this equation is known as the Characteristic polynomial) where you solve for values of λ. These values are your eigenvalue answers.
Plug in each eigenvector into
to find the eigenvectors
Notes:
- A negative eigenvector implies that a given eigenvector flips over 0,0 self (but still never changes off its span)
- A eigenvector of 1 means no stretching has occurred, means you can use it as a axis of rotation
- There may be no eigenvectors / only one (IE in a rotation matrix transformation)
- trying to calculate eigenvalues will result in imaginary numbers
Empathy
In the case of a A-1 * T * A set of transformation, where the outer A and A-1 matrices are used to transform a vector to our space then back to an alternate space, these outer matrices are called the Empathies
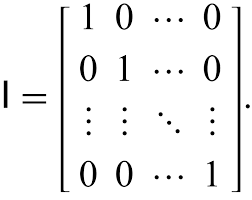
Identity Matrix
A square matrix composed of all zeros except for the forward diagonal which is all ones. Multiplying a matrix with an identity matrix results in the same original matrix, just as multiplying a number by "1" results in that same number.
- Important for finding Inverse Matrices
- Can only be square!
Inverse Matrix
Given (square) matrix A, multiplying A with its inverse (denoted as A⁻¹) results the identity matrix of the same dimensions. In other words -> A⁻¹A = I
- Since there is no such thing as dividing matrices, multiplying by the inverse matrix is used instead to factor out matrices when solving linear system of equations
- if a matrix has a determinate of 0 (not full rank), there is no inverse
- Example: There's no way to take a transformation that transforms a plane into a line, and find an inverse transformation that turns a line into a plane again
- Example: There's no way to take a transformation that transforms a plane into a line, and find an inverse transformation that turns a line into a plane again
Linear Combination
When you scale 2 vectors separately then add them together to get a vector output.
Linear Composition / Product
A combination of 2 Linear transformations in a specific sequence, which can be encoded itself as a singular linear transformation.
- Example: Combining a rotation, then a shear transformation, as a single transformation that applies both effects
Numerically, a composition of 2 transformations can be found by multiplying the 2 matrices together (where the first transformation is on the right side of the multiplication)
- Note: Order matters, Composition / Product of matrices is not a Commutative property
Linear Dependence / Independence
A vector is said to be linearly dependent if it could be added as a "basis" vector to an existing set of basis vector of a coordinate space, and not increase dimensionality. In other words, a dependent vector is already within the span of the basis vectors. Linear independence is the opposite, in that the vector was not part of the span and thus adding it as a basis vector allows for the span to increase in dimensionality
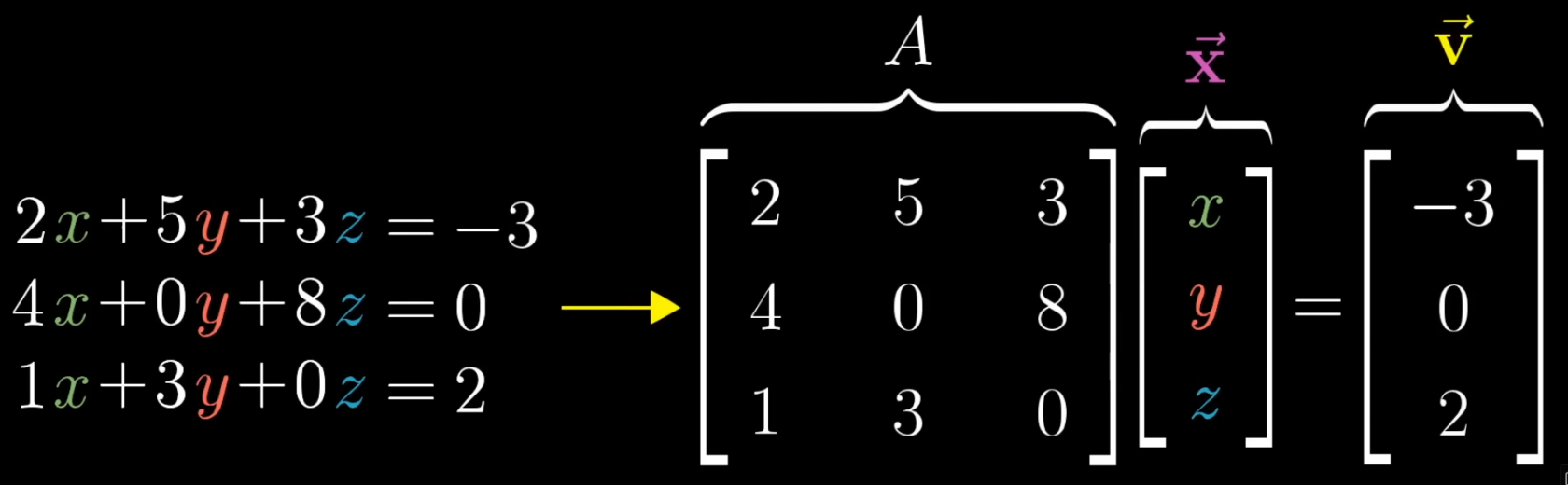
Linear Systems of Equations
A system of equations in which:
- Each variable is only multiplied by a scalar
- Remaining constants are factored on to the right side, while on the left side you keep your variables with scalars
- This format allows converting from a set of multiple equations, to a single equation using matrices to represent the values
- This shows an equation where we are looking for vector X that after transformation A, lands on vector V
- This is generally solved by using the inverse of A -> A⁻¹AX = A⁻¹V -> X = A⁻¹V
- ORDER MATTERS!
- This assumes that the determinate is nonzero, in which case there will always be one answer to the problem
- If the determinate is zero, it means the transformation is not full rank
- This means the inverse cannot be calculated, but there MAY still be a solution
- For a solution to exist, Vector V must exist on the reduced span area as a result of A
- If this is the case, then there are many solutions
- If not, there is no solution
- For a solution to exist, Vector V must exist on the reduced span area as a result of A
- This means the inverse cannot be calculated, but there MAY still be a solution
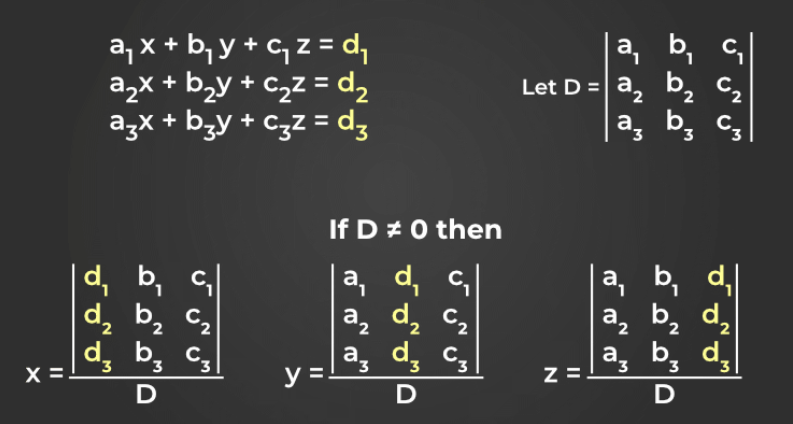
Cramer's Rule
A method for solving systems of equations as long as det(A) does not equal 0.
Linear Transformation
A function that transforms vector into a single other vector. Since they are used to map any number of input vectors to output vectors, we can use them to transform the space itself,
A transformation is only linear if the resultant space:
- Does not have its origin moved
- If all previously equidistant points remain equidistant
- parallel lines before remain parallel after
- Straight lines must remain straight
A Linear transformation can be described as a set of vectors that describe where the initial i and j (and k) basis vectors will land as a result of the transformation, they are often kept in an NxN matrix.
Null Space / Kernel
In the case on non-full rank transformations, multiple vectors become squished onto the 0,0 vector as a result, The space of all vectors that get squished here is known as the Null Space (or the Kernel).
Rank
an Integer that describes the number of dimensions the output of a transformation gives us.
- A rank of 1 is a line
- A rank of 2 is a plane
- A rank of 3 is a volume
If the number of dimensions going in is equal to the number of dimensions going out (a transform doesn't have a determinate of 0), we call the the transform "Full Rank"
Scalar
A non-vector, as in does not specify a direction. At most can only define a magnitude.
Scalar Multiplication with a Vector
Takes a scalar and a vector, and outputs a vector with the same number of dimensions. Commutative,
Geometric: Scales the magnitude of a vector without changing the direction (except in the case of negative scalars where the direction reverses)
Numeric: Multiply each element of a vector with the scalar to get an output,
Span
The set of all achievable vectors retrievable from every possible Linear Combination of a set of defined vectors. If the input vectors are on the same line / within the span of the other vectors, the dimensionality of the result will be reduced!
Vector Span
For Vectors, a span is the infinite line that can be found with one point on the origin, the other on the tip of a given vector. Multiplying that vector by any scalar will always result in the vector landing on its span,
Trace
The trace of a matrix of a matrix is the sum of all values along the diagonal of a matrix (Matrix does not need to be diagonal).
Vector
Geometric: A direction in space, where the numbers are the translation to go from the tail end of the vector to the head.
Numeric: An ordered set of numbers.
Vector Addition
Takes 2 vectors and outputs a vector.. Commutative. Both input vectors must have the same number of dimensions, Output vector will have the same number of dimensions.
Geometric: The result of following the motion of both input vectors, one after another
Numeric: Add like terms of the input to get the output.